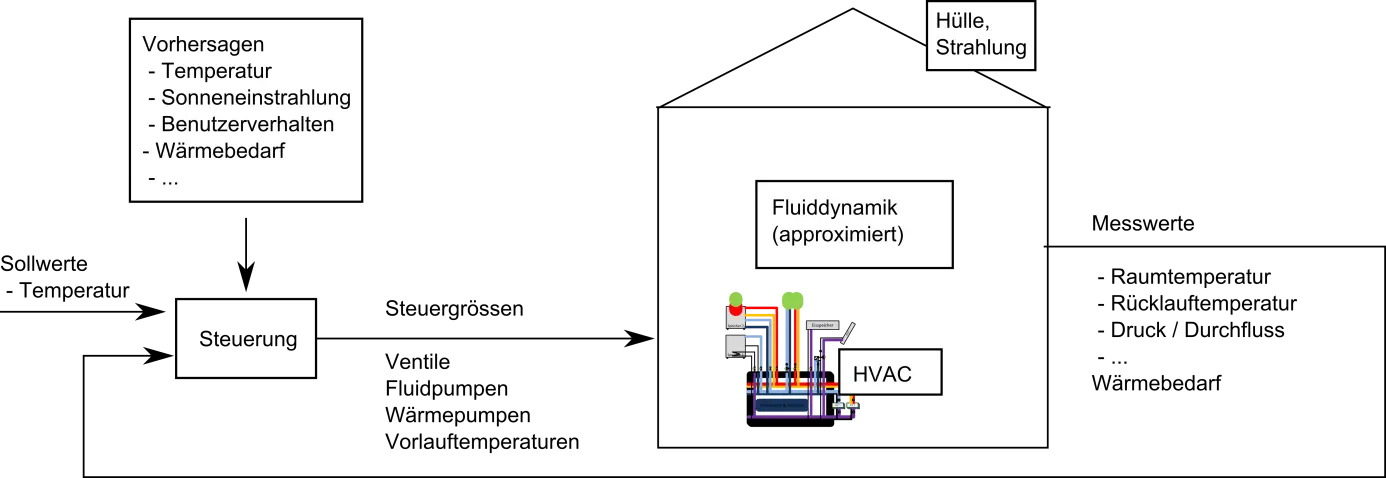
Multiscale Modeling
Multiscale-Modeling (MM) bezeichnet den Aufbau eines Systemmodells aus mehreren Teilmodellen auf unterschiedlichen Grössenskalen, die parallel zur Beschreibung unterschiedlicher Aspekte des Systemverhaltens verwendet werden. Hauptsächliche Motivation ist die Tatsache, dass Effekte auf der kleinsten verwendeten Skala („Mikroskala“) das Verhalten des Systems auf der eigentlich interessierenden makroskopischen Skala entscheidend beeinflussen, aber die Modellierung der gesamten Dynamik auf der Mikroskala aber zu aufwendig oder die Simulation zu komplex wäre.
MM besteht aus drei Komponenten[1]:
- Multiscale Analysis : Analyse des Grössenskalen und deren Zusammenspiel
- Multiscale Models : Modellierung der Teilmodelle sowie deren Kopplung
- Multiscale Algorithms : Implementierung geeigneter Algorithmen zur Realisierung und Simulation der Modelle
Projekterfahrung ACSS
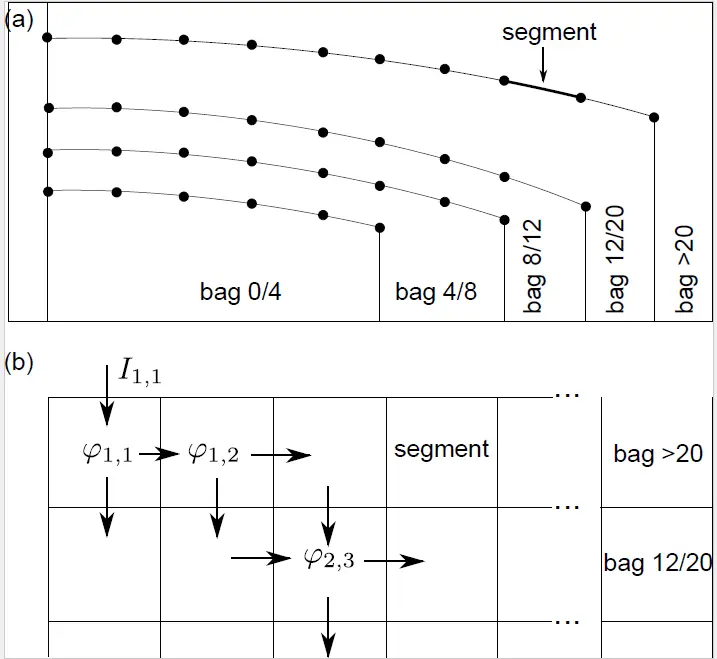
Es wurde ein erfolgreiches, KTI-gefördertes Projekt mit der AMMAN AG durchgeführt, das die Simulation und Optimierung industrieller Siebe zum Ziel hatte. Die betrachteten Siebe klassieren Kiesel mit Durchmessern zwischen <1mm bis >20mm Durchmesser in (beispielsweise) fünf Grössenklassen. Das Modell setzt sich aus Modellen der zwei Grössenskalen
- Mikroskopisch: Verhalten einzelner Kiesel auf einem Siebdeck
- Makroskopisch: Verhalten einer grossen Menge Kiesel
zusammen, wobei das mikroskopische Modell einzelne Kiesel mit ihrer Geometrie sowie die Interaktion mit anderen Kieseln für eine bescheidene Anzahl (in der Grössenordnung von 10^3 Kieseln) beschreibt, während das makroskopische Modell die Massenbilanz der Gesamtheit der Kiesel (in der Grössenordnung von 10^8 Kieseln) mit statistischen Kennzahlen betrachtet. Das Mikroskopische Modell liefert dabei die wichtigsten statistischen Kennzahlen als Eingangsparameter für das makroskopische Modell.
Die Implementierung der Algorithmen erfolgte dabei in auf einem handelsüblichen PC in Open-Source Umgebungen, nämlich YADE[2] für die mikroskopische und Octave[3] für die makroskopische Skala. Da insbesondere die Simulation der makroskopischen Modelle sehr effizient geschieht (der stationäre Zustand wird typischerweise nach wenigen Sekunden Simulationsdauer erreicht), kann ein Sieb sehr effizient simuliert werden. Die mikroskopische Simulation, die ca. eine Woche in Anspruch nahm, muss nicht für jedes Sieb wiederholt werden .
Projektbeispiel: Leistungsvorhersage und Optimierung für industrielle Siebmaschinen durch Simulation Aufgabe
Das Sieben ist das einfachste mechanische Klassierungsverfahren und zugleich ein Schlüsselprozess in der Asphaltherstellung. Für die Auslegung und den Betrieb industrieller Siebe spielen eine ganze Reihe von Parametern eine Rolle, die nach dem heutigen Stand der Technik im Wesentlichen aus Erfahrungswerten zum kleineren Teil auf Grund von – aufwendigen – Laborversuchen festgelegt werden.
Ein quantitatives Modell, das fundierte Vorhersagen über die Siebleistung macht, ermöglicht es, die Parameterauswahl zu optimieren und den Durchsatz und die Trenngüte der Anlage zu verbessern. Im vorliegenden Projekt wurde ein solches Modell erstellt und als simulierbares Computerprogramm implementiert.
Lösungsansatz und Ergebnis
Die Simulation einer Siebanlage mit einem Durchsatz in der Grössenordnung von Steinen pro Stunde ist auch mit modernen Rechnern nicht realistisch. Die vereinfachende Annahme, es handle sich beim Sieben um einen Prozess erster Ordnung mit konstanten Raten ist zu simpel und führt auf Ergebnisse, die deutlich von Messungen abweichen. Die im Projekt angewandte Methode ist eine Kombination aus einer Mehrteilchensimulation (Discrete Element Model, DEM) einerseits und einem makroskopischen Modell (Thick layer model, TLM) andererseits.
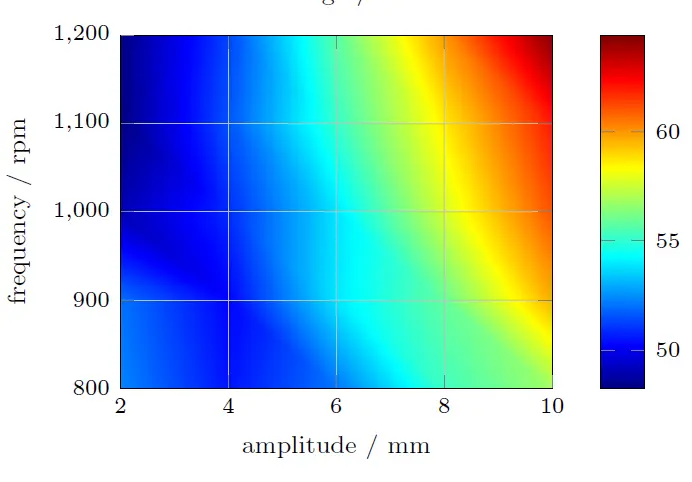
Das DEM simuliert einen kleinen Ausschnitt des Siebs und dient dazu, Transportgeschwindigkeiten und die Rate des Siebprozesses in Abhängigkeit verschiedener Parameter wie unter Anderem Schichtdicke, Vibrationsfrequenz und Vibrationsrichtung sowie Neigungswinkel zu bestimmen. Das DEM kann in einigen Tagen Rechenzeit die benötigten Ergebnisse für den zu betrachtenden Parameterbereich bestimmen und muss nur einmal verwendet werden.
Das DEM simuliert einen kleinen Ausschnitt des Siebs und dient dazu, Transportgeschwindigkeiten und die Rate des Siebprozesses in Abhängigkeit verschiedener Parameter wie unter Anderem Schichtdicke, Vibrationsfrequenz und Vibrationsrichtung sowie Neigungswinkel zu bestimmen. Das DEM kann in einigen Tagen Rechenzeit die benötigten Ergebnisse für den zu betrachtenden Parameterbereich bestimmen und muss nur einmal verwendet werden.
Diese Grössen dienen als Parameter für das TLM, welches auf Grund einer einfachen Massenbilanz die Trenngüte und den Durchsatz eines Siebs für gegebene Parameter berechnet. Dies geschieht innerhalb weniger Sekunden Rechenzeit.
Das Modell ist damit in der Lage äusserst schnell die Zusammenhänge zwischen den Design- und Betriebsparametern und der Trenngüte und dem möglichem Durchsatz zu bestimmen.
[1] Weinan, E. and Jianfeng, Lu (2011), Scholarpedia 6(10):11527