Softwarezuverlässigkeit und Dynamic Flowgraph Modelling
Im Rahmen eines Forschungsprojekts mit dem Kernkraftwerk Gösgen wurde in einer ersten Phase der Frage nach Softwarezuverlässigkeitsmodellen im allgemeinen und in einer zweiten Phase der Modellierungsmethode Dynamic Flowgraph Modelling im speziellen nachgegangen.
Die erste Phase umfasste unter anderem folgende Fragestellungen:
- Was ist der Stand der Technik zur Abschätzung der Fehlerrate in einem Software gestützten System?
- Wie werden Zuverlässigkeitsmodelle im Hinblick auf Software eingesetzt?
- Inwieweit lassen sich Leittechnikfunktionen wie sie in Kernkraftwerken zum Einsatz kommen mittels der Methode Dynamic Flowgraph Modelling (DFM) modellieren und analysieren?
Softwarezuverlässigkeitsmodelle
In einer ersten Phase wurde der aktuelle Stand der Technik sowie Forschungsaktivitäten in den Bereichen Softwarezuverlässigkeit, Systemmodellierung, Common Cause Fehler in digitalen Leitsystemen und formalen Methoden untersucht. Der Fokus lag dabei primär auf dem Sektor der Kernenergie, schloss Stand der Technik und Literatur zu Forschungsaktivitäten in anderen Sektoren jedoch nicht a-priori aus. Unter anderem umfasste diese Phase die Auseinandersetzung mit:
- Software Zuverlässigkeitsmodellen basierend auf Black-Box Modellen und nichthomogenen Poisson Prozessen:
- Jelinski-Moranda
- Goel-Okumoto
- Schneidewind
- Bayes’schen Modellen zur Einbeziehung von Expertenmeinung
- Dynamischen Modellierungstechniken:
- Dynamic Flowgraph Modelling
- Markov/CCMT Methodik
- Common Cause Fehlern in digitalen Leitsystemen
- Formalen Methoden zur Modellierung, Spezifikation, Analyse, Verifikation und Validation
Diese Resultate wurden der aktuellen Position einer Reihe von Zulassungsbehörden zu den Kernthemen probabilistische Behandlung softwarebedingter Systemausfälle sowie systematischer und Common Cause Fehler in digitalen Leitsystemen gegenübergestellt.
Dynamic Flowgraph Modelling (DFM)
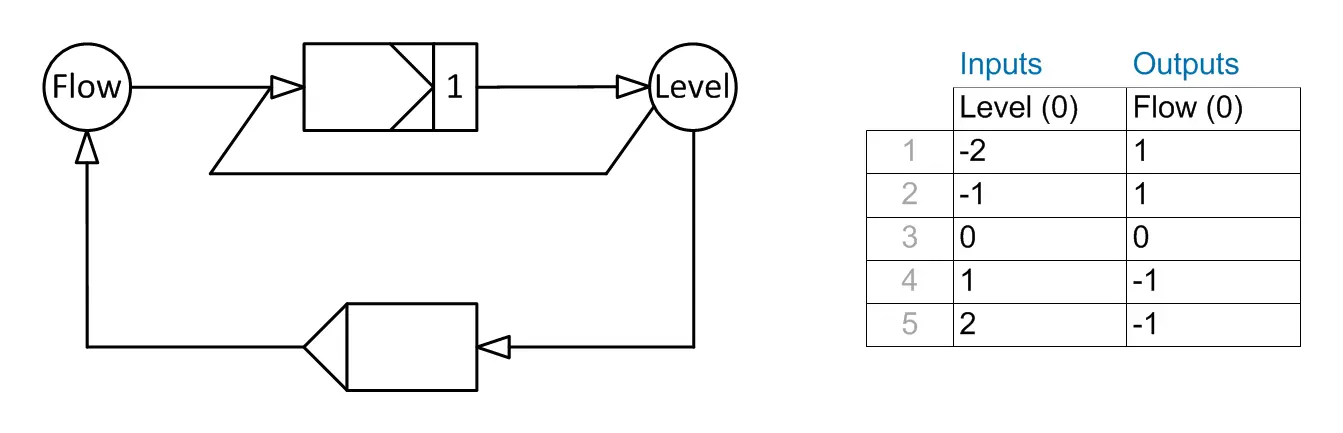
Mittels der DFM Methode können zeitabhängige Fehlerbäume generiert und analysiert werden. Dazu muss das System durch ein Modell dargestellt und im Zustandsraum und der Zeit diskretisiert werden, wobei die Übergänge zwischen den Zuständen dem Modell zusätzlich hinterlegt werden müssen. Die Diskretisierung ist ein wesentlicher Schritt im Modellierungsprozess: Einerseits soll die Zahl der Zustände klein gehalten werden, damit das System lösbar bleibt. Andererseits soll die Zahl aber hoch genug sein, damit das physikalische Verhalten mit dem notwendigen Detailgrad abgebildet werden kann.
DFM erlaubt es den gesamten Zustandsraum über den gesamten Zeitraum zu untersuchen. Die Analyse kann dabei Induktiv (vom Anfangs - zu den Endzuständen) oder deduktiv (vom Endzustand zu den auslösenden Zuständen, den sogenannten prime implicants) erfolgen. Jedem Endzustand („top event“) kann über die Eintrittswahrscheinlichkeit der prima implicants eine Wahrscheinlichkeit zugewiesen werden.
In einer zweiten Projektphase wurde DFM auf Leittechnikfunktionen angewendet: Die entsprechenden Systeme wurden modelliert und nach prime implicants spezifischer Fragen hin untersucht.
Auf einen Blick
Beteiligte Institute und Zentren:
Projektpartner:
Projektstatus: Abgeschlossen (2011)