Vertiefungsrichtung Computational Light Weight Design
In der Vertiefungsrichtung «Computational Light Weight Design» lernen Sie, innovative und nachhaltige Leichtbaustrukturen zu analysieren und zu optimieren. Dazu beschäftigen Sie sich einerseits mit analytischen und numerischen Berechnungsmethoden und -modellen und andererseits mit den dazu notwendigen Computertools. Die Vertiefung «Computational Light Weight Design» fokussiert auf die folgenden Themenfelder des Leichtbaus:
- Leichtbauweisen
- Materialmodelle von Leichtbauwerkstoffen
- Energiemethoden und Instabilitäten
- Ermüdungsfeste Dimensionierung
- Strukturmechanische Optimierungsmethoden
Warum Computational Light Weight Design studieren?
Knapper werdende Ressourcen, die Reduktion umweltschädlicher Schadstoffe und der stetig zunehmende globale Wettbewerb zwingen heutzutage praktisch jede Branche, ihre Produkte so leicht und kosteneffizient wie nur irgend möglich zu gestalten. Ingenieurinnen und Ingenieure mit fundierten Kompetenzen in der Auslegung gewichtsoptimierter Strukturen werden daher künftig in Konstruktions- und Berechnungsabteilungen noch gefragtere Experten sein, insbesondere wenn sie nicht nur die in der Industrie eingesetzten Computertools, sondern auch die Theorie dahinter kennen.
Die Vertiefungsrichtung «Computational Light Weight Design» behandelt ausgewählte Kapitel des Leichtbaus auf einem gehobenen theoretischen Niveau, wobei die Anwendung auf praktische und alltägliche Probleme der Ingenieurspraxis mittels Computertools wie Matlab, Python oder Abaqus demonstriert und geübt wird. Insofern eignet sich diese Vertiefungsrichtung für alle, die Spass an Festigkeitslehre, Finiten Elementen und numerischer Mathematik haben und gerne noch tiefer in die Strukturmechanik eintauchen möchten.
Wie ist die Vertiefungsrichtung aufgebaut?
Die Vertiefungsrichtung «Computational Light Weight Design» findet im 5. und 6. Semester des Bachelorstudiums statt.
Herbstsemester:
- 4 Lektionen pro Woche
- Davon je 2 Lektionen Theorie und Praktikum
Frühlingssemester:
- 4 Lektionen pro Woche
- Davon je 2 Lektionen Theorie und Praktikum
- 8 Lektionen numerisches Praktikum zur Strukturoptimierung
Wer kann sich für die Vertiefungsrichtung immatrikulieren?
- Bachelor MT ZHAW
- Interessierte Fachhörer
Welche Studieninhalte erwarten Sie?
Herbstsemester
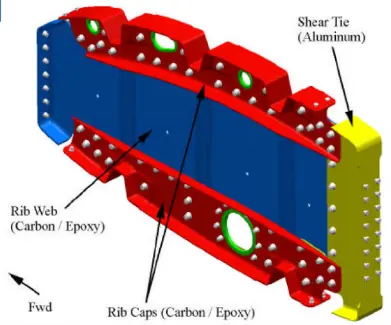
Leichtbauweisen
- Einführung in den Leichtbau
- Verschiedene Leichtbauweisen wie Monocoque, Semi-Monocoque und Fachwerk
- Beispiele aus dem Flugzeugbau
- Dimensionierungsbeispiele mit Matlab
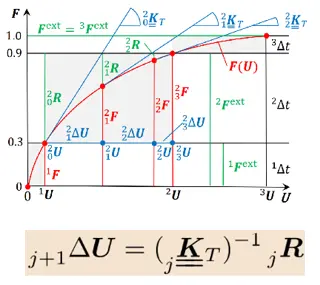
Nichtlineare FE-Methoden
- Einführung in nichtlineare FE-Methoden
- Ableitung des Newton-Raphson-Verfahrens anhand eines eindimensionalen Problems
- Newton-Raphson-Verfahren für physikalisch und geometrisch nichtlineare Probleme mit endlich vielen Freiheitsgraden
- Tangentensteifigkeitsmatrix
- Praktische Beispiele mit Matlab und Abaqus
Materialmodelle

Elastoplastisches Materialverhalten
- Plastizitäts- und Tangentenmodul
- Fliessfunktion, Fliessregel und Verfestigungsgesetz
- Der Prediktor-Korrektoralgorithmus
- Der Radial-Return-Algorithmus
- Praktische Beispiele mit Matlab und Abaqus
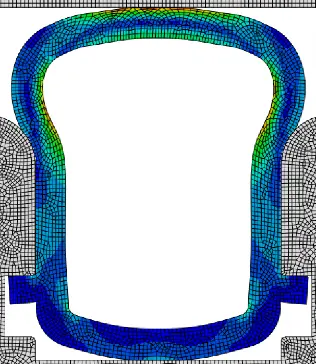
Hyperplastisches Materialverhalten
- Deformations- und Verschiebungsgradient
- Greenscher und Almansischer Verzerrungstensor
- Hyperelastisches Potential
- Neo-Hooke, Money-Rivlin und Ogden-Materialmodell
- Generierung und Kalibrierung von Materialdaten
- Praktische Beispiele mit Matlab und Abaqus
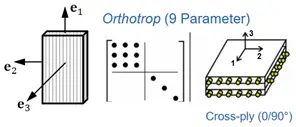
Orthotropes Materialverhalten
- Eigenschaften von Composites
- Lineare anisotrope Elastizität
- Effektive Materialparameter
- Elastizität von UD Lagen und Laminaten
- Versagensmechanismen und -kriterien
- Praktische Beispiele mit Matlab und Abaqus
Frühlingssemester
Frühlingssemester
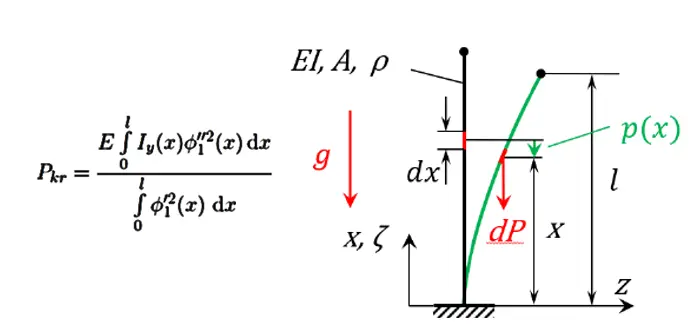
Energiemethoden und Instabilitäten
- Gleichgewichtsbedingungen am un- bzw. verformten System
- Lösung des Eigenwertproblems
- Formänderungsarbeit- und Energie
- Prinzip vom Minimum der totalen potentiellen Energie
- Das Verfahren von Ritz
- Das Phänomen der Instabilität
- Berechnung kritischer Lasten mittels des Raleighschen Quotienten
- Instabilitäten von Balken und Platten
- Auslegung mit Berücksichtigung von Instabilitäten
- Praktische Beispiele mit Matlab und Python
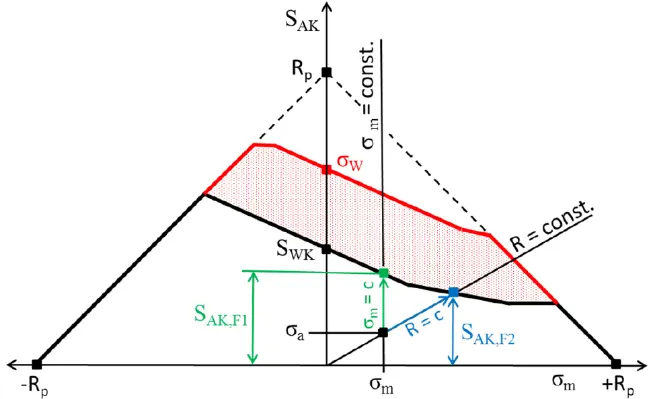
Ermüdungssichere Dimensionierung
- Einführung in die dauerfeste Auslegung nach dem Nennspannungskonzept
- Begriff der Kerbe, Formzahlen, Kerbwirkungszahl
- Konstruktive Einflüsse auf die Dauerfestigkeit
- Werkstoffseitige Einflüsse auf die Dauerfestigkeit
- Konstruktion von Haigh-Diagrammen
- Überlastfälle, Sicherheitsfaktoren, Auslastungsgrad
- Einführung in die Betriebsfestigkeit
- Minerregeln, Lastkollektive, Rainflow-Auszählungen
- Lebensdauerlinie und Betriebsfestigkeitsnachweis
- Praktische Beispiele mit Matlab

Strukturmechanische Optimierungsmethoden
- Algorithmen zur Optimierung
- Parameteroptimierung
- Topologieoptimierung
- Numerisches Praktikum I
- Numerisches Praktikum II
Welche Kompetenzen erwerben Sie in dem Vertiefungskurs?
- Sie lernen durch analytisches und computergestütztes Modellieren, Leichtbaukon-struktionen zu gestalten, zu dimensionieren und zu optimieren.
- Sie lernen, wie man komplexes Werkstoff- und Bauteilverhalten auf mathematische Modelle abstrahiert.
- Sie erweitern Ihr Wissen in FEM auf nichtlineare strukturmechanische Berechnungen.
- Sie lernen, unterschiedliche Disziplinen Ihres Studiums wie Analysis, Lineare Algebra, Statik, Festigkeistlehre, FEM, Numerische Mathematik und Programmieren miteinander zu verbinden, um gewichtsoptimierte Strukturen auszulegen.
- Sie vertiefen Ihre Toolkompetenzen in Matlab, Python und Abaqus.
- Sie erwerben wissenschaftlich-methodische Kompetenz, um bestehende technische Lösungen zu bewerten bzw. um neue Lösungen zu generieren.
Welche Qualifikationsarbeiten können Sie in Computational Light Weight Design schreiben?
Sie haben die Möglichkeit, folgende Arbeiten bei uns zu absolvieren:
- Projektarbeit (HS)
- Bachelorarbeit (FS)
- Vertiefungs-Arbeiten im Rahmen des MSE
- Masterarbeit im Rahmen des MSE (HS, FS)
Die Themen stammen dabei aus Forschungs- und Industrieprojekten und sind daher verknüpft mit relevanten und aktuellen Fragestellungen aus der Leichtbautechnik.
Wo finden Sie weiterführende Informationen?
Weitere Informationen zu den Studieninhalten finden Sie in den Modulbeschreibungen CLWD1 und CLWD2.
Bei Fragen wenden Sie sich an den Schwerpunktleiter Ralf Pfrommer: pfro@zhaw.ch