Additive manufacturing is a revolutionary developed technology playing an increasing role in various industries. Controlling the residual stresses is crucial to design the process in such a way that the manufactured piece meets the required properties. We build a general model of thermoelastic surface growth where the act of adding material to the boundary of the workpiece, is coupled with the heating effects during the solidification of the added material.

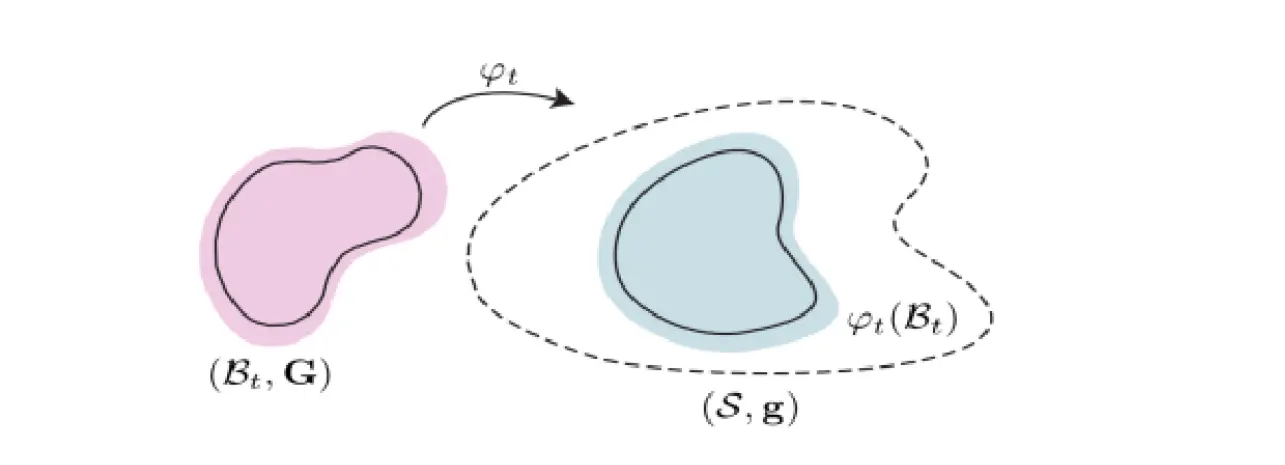
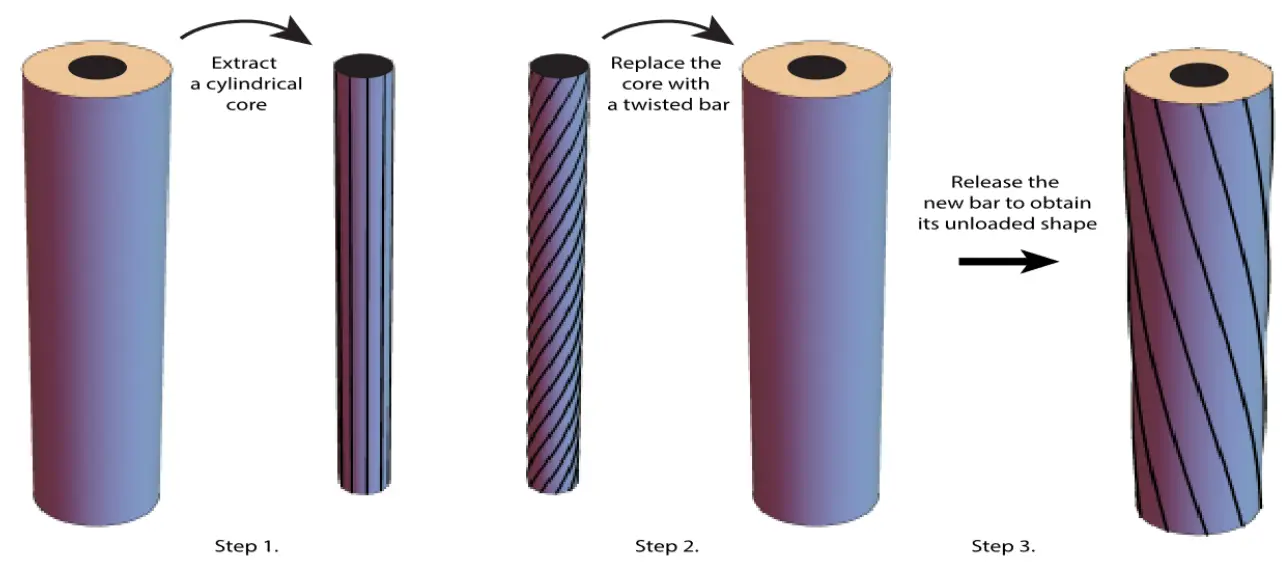
Additive manufacturing, most commonly known as 3D printing, has already found many applications in fields ranging all the way from hobbyist art to precise manufacturing in various industries such as mechanical, aerospace, and medical. Control of the residual stresses is crucial to tailor the process parameters in such a way that the manufactured piece meets the required properties in its working conditions. Indeed, the high temperatures and natural cooling to which the piece is subjected during the additive manufacturing process cause large strains and can result in a high level of residual stresses. This may lead to severe part distortion, dimensional inaccuracies, and even cracks in the final manufactured object. Such conditions put the additive manufacturing problem beyond the scope of the application of linearized elasticity. However, most of the existing computational works on additive manufacturing, are purely based on line arized elasticity, and use finite element analysis. Note that t.he boundary-value problems of accretion problems have not been formulated properly to this date and the mechanics of accretion at finite strains are still in their infancy. We build a general model of thermoelastic surface growth where surface growth, i.e., the act of adding material to the boundary of the workpiece, is coupled with the machine-induced heating and natural cooling during the solidification process of the added material. For such structures, a knowledge of the mechanical properties of the constituents in their stress-free configuration is not sufficient. The distribution of residual stresses explicitly depends on the accretion process, e.g., the initial temperature of the added material at the time of attachment, accretion velocity, history of loading, etc. Figure 1. In [1], a geometric theory of nonlinear accretion mechanics was introduced for a symmetric surface growth of cylindrical and spherical bodies. This theory was used for the analysis of several model problems. It was later generalized to non-symmetric accretion [2] and coupling with the heat equation [3]. In the proposed research program, the theory of [1,2] is being extended to analyze an accreting shaft made of a nonlinear elastic solid. This is a generalization of the twist-fit problem of nonlinear elasticity (see Figure 2). More specifically, we consider a finite circular shaft made of an incompressible solid that can be isotropic, transversely isotropic, or orthotropic in its relaxed state. We assume that this shaft is under a time-dependent torque T(t) while stress-free layers are printed on the cylindrical boundary of the shaft. We are interested in i) the residual stress distribution in the shaft, ii) its relaxed shape after unloading, iii) its response (stress distribution and angle of twist) under a given static torque after it is additively manufactured.

[1] F. Sozio and A. Yavari. Nonlinear mechanics of surface growth for cylindrical and spherical elastic bodies. Journal of the Mechanics and Physics of Solids, 98:12 – 48, 2017.
[2] F. Sozio and A. Yavari, Nonlinear mechanics of accretion, Journal of Nonlinear Science 29(4), 2019, 1813-1863.
[3] F. Sozio, M. F. Shojaei, S. Sadik, and A. Yavari, Nonlinear mechanics of thermoelastic accretion, Zeitschrift für Angewandte Mathematik und Physik (ZAMP) 71(3), 2020, 87.